Daily Practice Problems Relations and Functions

Question1:

For A = {10, 1, 2, 3} a relation R on A is defined as follows:

R = {(10, 10), (10, 1), (10, 3), (1, 10), (1, 1), (2, 2), (3, 10), (3, 3)}.

Check whether R is reflexive, symmetric or transitive?

Question2:

When we say that any relation for a set is an equivalence relation?

Question3:

For any set A = {x, y, z}, write the total number of equivalence relation.

Question4:

Let the function f : R → R be defined by f (x) = 2x – 2, ∀ x ∈ R. Then,

show that f is one-one.

Question5:

Every relation which is symmetric and transitive is also reflexive. Is it true or false? Justify with an example.

Question6:

Let R = {(3, 1), (1, 3), (3, 3)} be a relation defined on the set A = {1, 2, 3}. Then R is symmetric, transitive but not reflexive. Is it true or false? Justify your answer.

Question7:

Let the relation R be defined in W by xRy if 3x + 2y = 30. Then write R.

Question8:

If f(x) = x² + 2 and g(x) = x³ then find gof as well as fog.

Question9:

Find domain of the function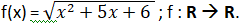

Question10:

If R = {(a, b): a + 2b = 10} is a relation defined on N, then write the range of R.

Question11:

Show that the function f : R → R defined by f (x) = (x²-2), ⩝ x ∈ R is neither one-one nor onto.

Question12:

Let L denote the set of all straight lines in a plane. Let a relation R be defined by lRm if and only if l is perpendicular to m ∀ l, m ∈ L. Then R is:

(a) Reflexive

(b) Symmetric

(d) None.

Question13:

Let A = {0, 1, 2, 3, ...n} and B = {-1, -2}. Then the number of surjections from A into B is:

(a) ⁿ⁺¹P₂

(b) 2ⁿ – 2

(d) 2ⁿ⁺¹ – 2

Question14:

If f = {(11, 21), (31, 51), (41, 11)} and g = {(21, 31), (51, 11), (11, 31)}. Then Find gof and fog.

Question15:

Let R be the set of real numbers and f : R → R be the function defined by f (x) = 5x + 5. Show that f is invertible and find f ^–1.

Question16:

Let R be the set of real numbers and f : R → R be the function defined by f (x) = x³ + 2. Show that f is invertible and find f ^–1.

Question17:

Let A = {1, 2, 3} and R be the smallest equivalence relation on A, then write R.

Question18:

Let A = {1, 2, 3} and B = {4, 5}. Then among the following subsets of A x B which are functions from A to B:

(i) f = {(1, 4), (1, 5), (2, 4), (3, 5)}

(ii) g = {(1, 4), (2, 4), (3, 4)}

(iii) h = {(1,4), (2, 5), (3, 5)}

(iv) k = {(1,4), (2, 5)}

Question19:

A relation R on the set {1, 2, 3} is defined as R = {(2, 3)}, then R is:

(a) reflexive

(b) transitive

(d) none of these.

Question20:

If the set A contains 4 elements and the set B contains 5 elements, then the number of one-one and onto mappings from A to B is:

(a) 625

(b) 60

(d) None of these

**********

Problem-solving on Class 12 Maths Relations and Functions NCERT Chapter 1 after learning a theoretical concept is crucial for several reasons:

Application of Knowledge: Problem-solving allows you to apply the theoretical concepts of the topic Class 12 Maths Relations and Functions you have learned to real-life situations. It helps you bridge the gap between abstract knowledge and practical scenarios, making the learning more relevant and meaningful.
Understanding Deeper Concepts: When you encounter problems related to a theoretical concept that you learned in Class 12 Maths Relations and Functions NCERT Chapter 1, you are forced to delve deeper into its intricacies. This deeper understanding enhances your comprehension of the subject and strengthens your grasp of the underlying principles.
Critical Thinking: Problem-solving encourages critical thinking and analytical skills. It requires you to analyze the problem, identify relevant information, and devise a logical solution. This process sharpens your mind and improves your ability to approach complex challenges effectively.
Retention and Recall: Actively engaging in problem-solving reinforces your memory and improves long-term retention. Applying the concepts learned in Relations and Functions Class 12 Maths in practical scenarios helps you remember them better than passive reading or memorization.
Identifying Knowledge Gaps: When you attempt to solve problems, you may encounter areas where your understanding is lacking. These knowledge gaps become evident during problem-solving, and you can then focus on filling those gaps through further study and practice. You can refer Relations and Functions Class 12 Maths Notes on LearnoHub.com
Boosting Confidence: Successfully solving problems after learning a theoretical concept boosts your confidence in your abilities to handle Relations and Functions. This confidence motivates you to tackle more challenging tasks and improves your overall performance in the subject.
Preparation for Exams and Challenges: Many exams, especially in science, mathematics, and engineering, involve problem-solving tasks. Regular practice in problem-solving prepares you to face these exams with confidence and perform well. It is also advised to take tests on Relations and Functions Class 12 Maths Online Tests at LearnoHub.com.
Enhancing Creativity: Problem-solving often requires thinking outside the box and exploring various approaches. This fosters creativity and innovation, enabling you to come up with novel solutions to different problems.
Life Skills Development: Problem-solving is a valuable life skill that extends beyond academics. It equips you with the ability to tackle various challenges you may encounter in personal and professional life.
Improving Decision Making: Problem-solving involves making decisions based on available information and logical reasoning. Practicing problem-solving enhances your decision-making skills, making you more effective in making informed choices.

In summary, problem-solving after learning a theoretical concept on CBSE Relations and Functions Class 12 Maths is an essential part of the learning process. It enhances your understanding, critical thinking abilities, and retention of knowledge. Moreover, it equips you with valuable skills that are applicable in academic, personal, and professional contexts.

You must have heard of the phrase “Practice makes a man perfect”. Well, not just a man, practice indeed enhances perfection of every individual.

Practicing questions plays a pivotal role in achieving excellence in exams. Just as the adage goes, "Practice makes perfect," dedicating time to solve a diverse range of exam-related questions yields manifold benefits. Firstly, practicing questions allows students to familiarize themselves with the exam format and types of problems they might encounter. This familiarity instills confidence, reducing anxiety and improving performance on the actual exam day. Secondly, continuous practice sharpens problem-solving skills and enhances critical thinking, enabling students to approach complex problems with clarity and efficiency. Thirdly, it aids in identifying weak areas, allowing students to focus their efforts on improving specific topics. Moreover, practice aids in memory retention, as active engagement with the material reinforces learning. Regular practice also hones time management skills, ensuring that students can allocate appropriate time to each question during the exam. Overall, practicing questions not only boosts exam performance but also instills a deeper understanding of the subject matter, fostering a holistic and effective learning experience.

All About Daily Practice Problems on Class 12 Maths Relations and Functions NCERT Chapter 1

Our Daily Practice Problems (DPPs) offer a diverse range of question types, including Multiple Choice Questions (MCQs) as well as short and long answer types. These questions are categorized into Easy, Moderate, and Difficult levels, allowing students to gradually progress and challenge themselves accordingly. Additionally, comprehensive solutions are provided for each question, available for download in PDF format - Download pdf solutions as well as Download pdf Questions. This approach fosters a holistic learning experience, catering to different learning styles, promoting self-assessment, and improving problem-solving skills. With our well-structured DPPs, students can excel in exams while gaining a deeper understanding of the subject matter. Hope you found the content on Class 12 Maths Relations and Functions NCERT Chapter 1 useful.

Last but not least, to get the best hold on Class 12 Maths Relations and Functions NCERT Chapter 1, do not forget to check out:

Relations and Functions Class 12 Maths Best videos
Relations and Functions Class 12 Maths NCERT Solutions
Class 12 Maths Relations and Functions Revision notes
Relations and Functions Class 12 Maths DPPs, Download PDF of solutions
Class 12 Maths Relations and Functions Online Tests
Class 12 Maths Sample papers