Sample paper maths

Sample Paper
Class 10 Maths
Sample Paper 4 | Class 10 Maths

Maximum Marks : 80 Taken : 3 Hours

General Instructions:

(i) All the questions are compulsory.

(ii) The question paper consists of 40 questions divided into 4 sections A, B, C, and D.

(iii) Section A comprises of 20 questions of 1 mark each. Section B comprises of 6 questions of 2 marks each. Section C comprises of 8 questions of 3 marks each. Section D comprises of 6 questions of 4 marks each.

(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, three questions of 3 marks each, and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.

(v) Use of calculators is not permitted.

SECTION - A

(Q1- Q10) Multiple Choice Questions

Question 1:

If angles A, B, C of a ΔABC are in AP, then the value of sin B is

(a)

(b) 1

(c)

(d)

Question 2:

In an AP, given a = 5, d = 3, a_n = 50, then the value of n is

(a) 10

(b) 16

(d) 32

Question 3:

For what value of k, the quadratic equation x² - kx + 4 = 0 has equal roots?

(a) ±1

(b) ±2

(d) ±4

Question 4:

If the distance between (5, 2p) and (2, 0) is 5, then the value of p is

(a) ±1

(b) ±2

(d) ±4

Question 5:

The HCF of any two consecutive numbers is

(a) 1

(b) 2

(d) none of these

Question 6:

One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting the queen of diamonds is

(a)

(b)

(c)

(d)

Question 7:

If the perimeter and area of a circle are numerically equal, then the radius of the circle is

(a) 2 units

(b) π units

(d) 7 units

Question 8:

Find the value of tan P – cot R in the given figure.

(a) 0

(b)

(c)

(d) 1

Question 9:

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Then the height of the tower is

(a) 21 m

(b) 28 m

(d) 42 m

Question 10:

The value of k if the quadratic polynomial 2x² - 3kx + 5 has 9 as the sum of zeroes

(a) 2

(b) 4

(d) 8

(Q 11- Q 15) Fill in the blanks

Question 11:

In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Then the length of the arc is _________.

Question 12:

If the 17^th term of an AP exceeds its 10^th term by 7 then the common difference is _________.

Question 13:

In a ΔABC, if ∠C = 3∠B = 2(∠A + ∠B) then the value of ∠A is ______.

Question 14:

If the mean of the observations x + 1, x + 4, x + 5, x + 8 and x + 11 is 10, the mean of the last three observations is ______.

Question 15:

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is _____.

(Q 16- Q 20) Answer the following:

Question 16:

If the mean of first n natural number is 15 then what is the value of n?

Question 17:

If the difference between two numbers is 26 and one number is three times the other, then find them.

Question 18:

If Q(0, 1) is equidistant from P(5, –3) and R(x, 6) then find the values of x.

Question 19:

Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together ?

Question 20.:

The perimeter of two similar triangles ABC and LMN are 60 cm and 48 cm respectively. If LM = 8 cm then what is the value of AB?

SECTION – B

Question 21:

A quadrilateral ABCD is drawn to circumscribe a circle as shown in the figure. Prove that: AB + CD = AD + BC

Question 22:

The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30⁰ than when it was 60⁰. Find the height of the tower. (Given √3 = 1·732)

Question 23:

A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is

(i) a card of spade or an ace. (ii) a black king.

Question 24:

A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Question 25:

The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Question 26:

There are 50 numbers. Each number is subtracted from 53 and the mean of the numbers so obtained is found to be –3.5. Determine the mean of the given numbers.

SECTION - C

Question 27:

Prove that 3 + 2√2 is an irrational number, given that √2 is an irrational number.

Question 28:

If the sum of the first n terms of an AP is 4n - n², what is the first term (that is S₁)? Also, find the nth terms.

Question 29:

A train covered a certain distance at a uniform speed. If the train would have been 10 faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 ; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.

Question 30:

Find the zeroes of the quadratic polynomial 6x² – 3 – 7x and verify the relationship between the zeroes and the coefficients.

Question 31:

If tan(A + B) = √3 and tan(A - B) = 1, 0° < A + B < 90° and A > B then find the value of A and B.

Question 32

The diagonals of a quadrilateral ABCD intersect each other at the point O such that . Show that ABCD is a trapezium.

Question 33:

A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm³ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?

Question 34:

The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.

SECTION - D

Question 35:

At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30°. The angle of depression of the reflection of the cloud in the lake, at a A is 60°. Find the distance of the cloud from A.

Question 36:

The HCF of 65 and 117 is expressible in the form 65p - 117. Find the value of p. Also find the LCM and HCF of 65 and 117 using prime factorisation method.

Question 37:

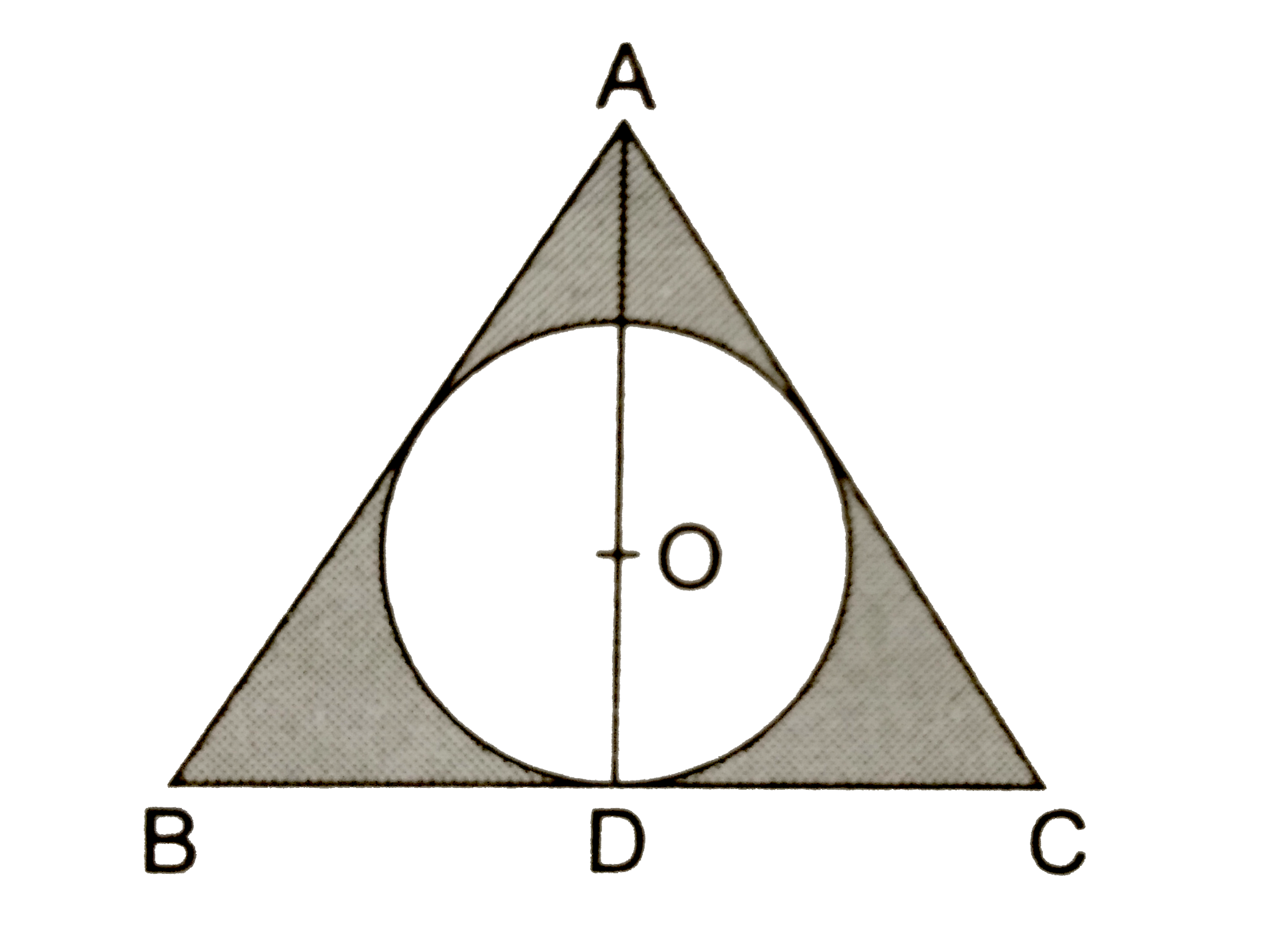
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of the inscribed circle and the area of the shaded region. [Use π = 3.14 and √3 = 1.732]

Question 38:

The following table gives production yield per hectare of wheat of 100 farms of a village.

Change the distribution to a more than type distribution, and draw its ogive.

Question 39:

Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Question 40:

Evaluate the following:

(i) (ii)

**********

Solving sample papers of Class 10 Physics, Chemistry, Maths, Biology, SST before exams is highly important and beneficial for several reasons: